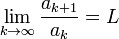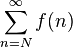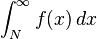Disco Selena Gomez 2011
Descargar: http://www.mediafire.com/?6k46a129qs9aoht
lunes, 18 de julio de 2011
jueves, 9 de junio de 2011
Evaluacion Parcial
Por medio de la presente se otorga el 90 % en los 5 subtemas del la unidad 3
miércoles, 8 de junio de 2011
3.1.2 Area Entre las Graficas de Funciones
Una forma para hallar el área delimitada entre dos funciones, es utilizando el cálculo integral:
f(x) y g(x)[<f(x)] y en el intervalo [a,b] .
Ejemplo Si se quiere hallar el área delimitada entre el eje x y la función f(x) = 4 − x2 en el intervalo [ − 2;2], se utiliza la ecuación anterior, en este caso: g(x) = 0 entonces evaluando la integral, se obtiene:
Ejemplo de Aplicación 1:
Ejemplo De Aplicacion 2:
La figura 5 hace la función de representar el área desarrollada anteriormente:
Fuentes:
3.2 Longitud De Curvas
La longitud de arco de una curva, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas, la llegada del calculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.
La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible. , escogiendo una familia finita de puntos en C, y aproximar la longitud mediante la longitud de la poligonal que pasa por dichos puntos.Cuantos más puntos escojamos en C, mejor seria el valor obtenido como aproximación de la longitud de C.
Video explicando 1 ejemplo de longitud del arco de una curva:
Fuente:http://www.youtube.com/watch?v=QLFhBPOtF4shttp://www.vadenumeros.es/segundo/area-grafica-de-dos-funciones.htm![]()
jueves, 2 de junio de 2011
3.4 Calculo de centroides
Calculo de la Centroides por medio de la integración.
1. Preparar un esquema del cuerpo a escala.
2. Establecer un sistema de coordenadas, en la mayoría de los cuerpos que sean superficies planas, se utilizan coordenadas rectangulares, siempre que el cuerpo presente un eje o un plano de simetría se tomara uno de los ejes, el centroide se encontrara siempre sobre tal eje.
3. Seleccionar un elemento de volumen , superficie o longitud.. para la determinación del centro de masa o centro de gravedad determinar la masa o el peso del elemento utilizando la expresión adecuada de la densidad o del peso especifico.
4. Escribir una expresión del primer momento del elemento respecto a uno de los ejes o planos de referencia. Integrar la expresión para determinar el primer momento.
5. Utilizar la ecuación adecuada para obtener las coordenadas del centroide.
6. Repetir los pasos del 3 al 5 con las coordenadas obtenidas.
Otras integrales
A pesar de que las integrales de Riemann y Lebesgue son las definiciones más importantes de integral, hay unas cuantas más, por ejemplo:
* La integral de Riemann-Stieltjes, una extensión de la integral de Riemann.
* La integral de Lebesgue-Stieltjes, desarrollada por Johann Radon, que generaliza las integrales de Riemann-Stieltjes y de Lebesgue.
* La integral de Daniell, que incluye la integral de Lebesgue y la integral de Lebesgue-Stieltjes sin tener que depender de ninguna medida.
* La integral de Henstock-Kurzweil, definida de forma variada por Arnaud Denjoy, Oskar Perron, y Jaroslav Kurzweil, y desarrollada por Ralph Henstock.
* La integral de Darboux, que es equivalente a la integral de Riemann.
* La integral de Haar, que es la integral de Lebesgue con la medida de Haar.
* La integral de McShane.
* La integral de Buchner
Otras aplicaciones para las integrales.
* Área entre curvas.
* Sólidos de revolución.
* Longitud de curvas.
Aqui una pequeña definicion y un ejemplo de como calcular un centroide:
miércoles, 1 de junio de 2011
3.5 otras aplicaciones
Aplicaciones de la Integral
Dentro de los problemas típicos que se pueden expresar de manera directa mediante integrales y complementarios al problema básico de “área bajo la curva” se tienen:
· Área entre curvas.
· Sólidos de revolución.
· Longitud de curvas.
· Centroides de figuras planas.
· Momentos de Inercia de cuerpos planos.
El objetivo de la presente sección es estudiar cada una de esas diferentes aplicaciones y se comenzará con la aplicación más común y que a su vez motivó los conceptos básicos de la integral: el área bajo la curva.
Área entre la curva y el eje x
En efecto, ya lo hemos señalado, integral no es lo mismo que área, ya que el concepto de integral es realmente un concepto mucho más amplio y que se puede aplicar a infinidad de situaciones novedosas. Por otro lado, realizando las correcciones necesarias respecto de los valores negativos que pueda tomar una función en un intervalo la integral calcula perfectamente el área entre el eje x y una curva dada.
Pero el concepto de área se puede ampliar a espacios delimitados entre diversas curvas en el plano, estudiemos ahora esa generalización.
Área entre curvas
La integral representa la acumulación de las pequeñas variaciones en una situación dada, por ello podemos responder a la pregunta: Si se tiene una curva ¿Cuánto mide? ¿Cómo la mido? ¿Qué son las pequeñas variaciones en ese caso?
Longitud de una curva
La integral como concepto nace alrededor del cálculo numérico, por lo que muchas de las integrales que se nos presentan en la vida cotidiana ni tan siquiera son planteadas analíticamente; sin embargo, eso no las hace inútiles; ¡por el contrario! El potencial analítico de la integral se logra ante la simplicidad del concepto ¡no deja de ser una suma!!!!!
Pero ahora con las computadoras, esas sumas las podemos hacer de manera muy eficiente.
Integración numérica
Es verdad que la motivación del la integración lo fue el concepto geométrico de área, pero ya hemos concluido que en realidad la podemos emplear en cualquier situación que se pueda representar por el producto de dos cantidades y el volumen es uno de esos casos, veamos los siguientes cuerpos geométricos y como la integral nos auxilia a calcular volúmenes.
Superficies y sólidos de Revolución
En los cuerpos físicos ocurren muchos fenómenos asociados a su geometría, dentro de esos fenómenos se presenta la ocurrencia de la masa, el peso y por tanto los efectos de la atracción gravitatoria, observemos ahora dos conceptos físicos necesarios para el estudio de cantidades físicas como las mencionadas.
Momentos de Inercia
Las aplicaciones de la integral son muy amplias y en este apartado se han presentado algunas de las más comunes, y con este estudio se amplia el panorama para que en nuestra visión de la naturaleza, en los actos que nos rodean todos los días, observemos como la acumulación es un hecho cotidiano.
martes, 31 de mayo de 2011
4.1 Definición de serie
En matemáticas, una serie es la suma de los términos de una sucesión.
Se representa una serie con términos an como
Siendo N es el índice final de la serie.
Siendo N es el índice final de la serie.
Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales.
Las series convergen o divergen.
Una serie diverge si
No existe o si tiende a infinito;
Converge si:
Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir, .
Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si para algún .
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de y se verifica es . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
Serie infinita
Primer ejemplo. Para alguna , sea y . Entonces
Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si para algún .
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de y se verifica es . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
Serie infinita
Primer ejemplo. Para alguna , sea y . Entonces
por definición y la fórmula binomial. Dado que, formalmente, y , se ha demostrado que . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo .
Segundo ejemplo. Sea x(n) = 1 para todo . Entonces C(x,x)(n) = n + 1 para todo por lo tanto el producto de Cauchy y no es convergente.
Evaluacion Parcial
Por medio de la presente informo que el equipo obtuvo el 93% de los 6 subtemas publicados.
Atte.
Ing.Jose Enrique Marquez Eloiza
Atte.
Ing.Jose Enrique Marquez Eloiza
lunes, 30 de mayo de 2011
4.2 SERIE NUMERICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (criterio de D´Alembert) y PRUEBA DE LA RAÍZ (criterio de Cauchy).
SERIE NUMERICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (criterio de D´Alembert) y PRUEBA DE LA RAÍZ (criterio de Cauchy).
Imaginemos que se va a celebrar una carrera con las siguientes reglas:
1. El primer minuto debe recorrerse 100 metros.
2. El minuto siguiente debe recorrerse la mitad, 50 metros.
3. El minuto siguiente debe recorrerse la mitad del anterior, 25 metros.
4. El minuto siguiente dee recorrerse la mitad del anterior, 12,50 metros.
y as´ı sucesivamente.
Por otra parte, al mismo tiempo empieza otra carrera, con las reglas ligeramente
modificadas:
1. El primer minuto se recorren 100 metros.
2. El minuto siguiente se recorren la mitad de 100 metros, 50 metros.
3. El minuto siguiente se recorren la tercera parte de 100 metros, 33,3
metros.
4. El minuto siguiente se recorren la cuarta parte de 100 metros, 25 metros.
y as´ı sucesivamente.
Dos corredores empiezan a la vez las carreras. Si la meta de la primera se
encuentra situada a 300 metros y la de la segunda a 1000 metros, ¿qui´en
llega primero a la meta y cu´anto tiempo tarda?
Llamamos D = 100 metros la distancia recorrida en el primer minuto. La
primera carrera va recorriendo las distancias:
D +D/2+D/4+D/8+ . . .
La segunda carrera va recorriendo las distancias:
D +D/2+D/3+D/4+ . . .
La pregunta es cu´al de estas sumas alcanza la distancia a la que est´a situada
la meta respectiva. Al acabar este tema deberemos ser capaces de dar una
respuesta razonada1.
Series de Convergencia
Son aplicables en caso de disponer de otra serie tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:

CONVERGENCIA
Criterio de D'Alembert
Criterio de Cauchy
 converge
converge
Imaginemos que se va a celebrar una carrera con las siguientes reglas:
1. El primer minuto debe recorrerse 100 metros.
2. El minuto siguiente debe recorrerse la mitad, 50 metros.
3. El minuto siguiente debe recorrerse la mitad del anterior, 25 metros.
4. El minuto siguiente dee recorrerse la mitad del anterior, 12,50 metros.
y as´ı sucesivamente.
Por otra parte, al mismo tiempo empieza otra carrera, con las reglas ligeramente
modificadas:
1. El primer minuto se recorren 100 metros.
2. El minuto siguiente se recorren la mitad de 100 metros, 50 metros.
3. El minuto siguiente se recorren la tercera parte de 100 metros, 33,3
metros.
4. El minuto siguiente se recorren la cuarta parte de 100 metros, 25 metros.
y as´ı sucesivamente.
Dos corredores empiezan a la vez las carreras. Si la meta de la primera se
encuentra situada a 300 metros y la de la segunda a 1000 metros, ¿qui´en
llega primero a la meta y cu´anto tiempo tarda?
Llamamos D = 100 metros la distancia recorrida en el primer minuto. La
primera carrera va recorriendo las distancias:
D +D/2+D/4+D/8+ . . .
La segunda carrera va recorriendo las distancias:
D +D/2+D/3+D/4+ . . .
La pregunta es cu´al de estas sumas alcanza la distancia a la que est´a situada
la meta respectiva. Al acabar este tema deberemos ser capaces de dar una
respuesta razonada1.
Series de Convergencia
Son aplicables en caso de disponer de otra serie
 tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
Criterio de comparación directa ( de la mayorante o de Gauss )
Si 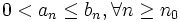
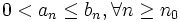
- Si
 converge
converge  converge
converge - Si
 diverge
diverge  diverge
diverge
Criterio de comparación por paso al límite del cociente

Entonces:
- Si L = 0 y
 converge
converge  converge
converge - Si
 y
y  diverge
diverge  diverge
diverge - En otro caso, ambas series comparten la misma condición (ambas convergen, o bien ambas son divergentes).
CONVERGENCIA
Una serie alternada an converge absolutamente si

es una serie convergente. Se demuestra que una serie que converge absolutamente, es una serie convergente.
Criterio de D'Alembert
Sea una serie  , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
 , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).Si existe
con 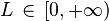 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
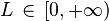 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.
- si L > 1, entonces la serie diverge.
- si L = 1, no es posible decir algo sobre el comportamiento de la serie.
En este caso, es necesario probar otro criterio, como el criterio de Raabe
Criterio de Cauchy
Si f(x) es una función positiva y monótonamente decreciente definida en el intervalo [1, ∞) tal que f(n) = an para todo n, entonces  converge si y sólo si
converge si y sólo si  es finita.
es finita.
 converge si y sólo si
converge si y sólo si  es finita.
es finita.Más generalmente, y para el tipo de función definida antes, pero en un intervalo [N,∞), la serie
converge si y sólo si la integral
converge
Sea 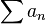 una serie monótona de números positivos decrecientes.
una serie monótona de números positivos decrecientes.  converge si y sólo si la serie
converge si y sólo si la serie
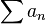 una serie monótona de números positivos decrecientes.
una serie monótona de números positivos decrecientes.  converge si y sólo si la serie
converge si y sólo si la serie converge
convergeBIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Serie_matemática#Criterio_de_D.27Alembert_o_Criterio_del_Cociente_.28Criterio_de_la_raz.C3.B3n.29
MC. Marcel Ruiz Martínez
jueves, 26 de mayo de 2011
Evaluacion parcial
El equipo obtuvo el 99% de la realizacion del trabajo.
4.3 Serie de potencias
Series de potencias. Desarrollos en serie
de Taylor
En la representación (e incluso en la construcción) de funciones, desempeñan un papel especialmente
destacado cierto tipo de series, denominadas series de potencias. Los aspectos profundos de su
estudio corresponden a la teoría de funciones de variable compleja más que a la teoría de funciones
de variable real, por lo que aquí damos simplemente algunas propiedades sencillas, suficientes para
nuestros propósitos.Series de potencias. Convergencia de las series de potencias. Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n.
El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término
n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n.
En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los
polinomios.
¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos.
Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x " (−1,1) (con suma 1 1−x , como sabemos).
de Taylor
En la representación (e incluso en la construcción) de funciones, desempeñan un papel especialmente
destacado cierto tipo de series, denominadas series de potencias. Los aspectos profundos de su
estudio corresponden a la teoría de funciones de variable compleja más que a la teoría de funciones
de variable real, por lo que aquí damos simplemente algunas propiedades sencillas, suficientes para
nuestros propósitos.Series de potencias. Convergencia de las series de potencias. Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n.
El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término
n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n.
En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los
polinomios.
¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos.
Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x " (−1,1) (con suma 1 1−x , como sabemos).
b) La serie ∞Σ n=1 xn n converge si y solo si x " [−1,1). Si x " (−1,1), converge absolutamente.
c) La serie ∞Σ n= xn n2 converge (absolutamente) si y solo si x " [−1,1].
d) La serie ∞Σ n=1(−1)nx2nn converge si y solo si x " [−1,1]. Si x " (−1,1), converge absolutamente.
e) La serie∞Σn=0xnn!converge (absolutamente) para todo x " R (y la suma es ex).
f) La serie∞Σn=0n!xn converge solamente para x = 0. Si para algún r " (0,+∞) la sucesión (anrn) está acotada, entonces para cada x " R tal que |x−c| < r la serie ∞Σ n=0 an(x−c)n es absolutamente convergente.
c) La serie ∞Σ n= xn n2 converge (absolutamente) si y solo si x " [−1,1].
d) La serie ∞Σ n=1(−1)nx2nn converge si y solo si x " [−1,1]. Si x " (−1,1), converge absolutamente.
e) La serie∞Σn=0xnn!converge (absolutamente) para todo x " R (y la suma es ex).
f) La serie∞Σn=0n!xn converge solamente para x = 0. Si para algún r " (0,+∞) la sucesión (anrn) está acotada, entonces para cada x " R tal que |x−c| < r la serie ∞Σ n=0 an(x−c)n es absolutamente convergente.
4.4 Radio de convergencia.
Definición
Si nos limitamos al conjunto de los números reales, una serie de la forma \sum_{n=0} a_n(x-x_0)^n, con a_n,x,x_0\in\mathbb{R}, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0.
Ejemplo:
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
[editar] Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
\frac{1}{1-x}=\sum_{n=0}^\infty x^n=1+x+x^2+x^3+....
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
\sum_{n=0}^\infty 0.25^n=1+0.25+0.25^2+0.25^3+...=\frac{4}{3}.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
\frac{1}{1-0.25}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
\sum_{n=0}^\infty 2^n=1+2+2^2+2^3+...=\infty.
[editar] Distancia a la singularidad
El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x0 = 3 tiene la forma:
\frac{1}{1-x}=-\frac{1}{2}+\frac{x-3}{4}-\frac{(x-3)^2}{8}+\frac{(x-3)^3}{16}-....
Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:
\frac{1}{1+x^2}=\frac{1}{2}-\frac{x-1}{2}+\frac{(x-1)^2}{4}-\frac{(x-1)^4}{8}+\frac{(x-1)^5}{8}-...
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es r=\sqrt{2}/2. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador. Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho e^{x}=\sum_{n=0}^\infty x^n/n!=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+.... y esto vale para todo real x por eso el radio de convergencia será infinito.
[editar] Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
\frac{1}{1-x}=\sum_{n=0}^\infty x^n=1+x+x^2+x^3+....
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
\sum_{n=0}^\infty 0.25^n=1+0.25+0.25^2+0.25^3+...=\frac{4}{3}.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
\frac{1}{1-0.25}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
\sum_{n=0}^\infty 2^n=1+2+2^2+2^3+...=\infty.
[editar] Distancia a la singularidad
El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x0 = 3 tiene la forma:
\frac{1}{1-x}=-\frac{1}{2}+\frac{x-3}{4}-\frac{(x-3)^2}{8}+\frac{(x-3)^3}{16}-....
Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:
\frac{1}{1+x^2}=\frac{1}{2}-\frac{x-1}{2}+\frac{(x-1)^2}{4}-\frac{(x-1)^4}{8}+\frac{(x-1)^5}{8}-...
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es r=\sqrt{2}/2. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador. Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho e^{x}=\sum_{n=0}^\infty x^n/n!=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+.... y esto vale para todo real x por eso el radio de convergencia será infinito.
Suscribirse a:
Entradas (Atom)